Skip to contents

BKP

The BKP package provides scalable Bayesian modeling tools for binomial and multinomial response data via the Beta Kernel Process (BKP) and its generalization, the Dirichlet Kernel Process (DKP).

  • BKP is designed for binary (or binomial) outcomes.
  • DKP extends BKP to handle multi-class responses via Dirichlet-multinomial modeling.

Both models leverage kernel-based weighting and conjugate priors to enable efficient posterior inference, probabilistic prediction, and uncertainty quantification.

Installation

You can install the stable version of BKP from CRAN with:

Or install the development version from GitHub with:

# install.packages("pak")
pak::pak("Jiangyan-Zhao/BKP")

BKP: Binary/Count Response Modeling

Example 

library(BKP)

# Simulate data
set.seed(123)
n <- 30
Xbounds <- matrix(c(-2, 2), nrow = 1)
x <- matrix(seq(-2, 2, length.out = n), ncol = 1)
true_pi <- (1 + exp(-x^2) * cos(10 * (1 - exp(-x)) / (1 + exp(-x)))) / 2
m <- sample(50:100, n, replace = TRUE)
y <- rbinom(n, size = m, prob = true_pi)

# Fit BKP model
model <- fit.BKP(x, y, m, Xbounds = Xbounds)

# Predict on new data
Xnew <- matrix(seq(-2, 2, length.out = 100), ncol = 1)
pred <- predict(model, Xnew)

# Plot results
plot(model)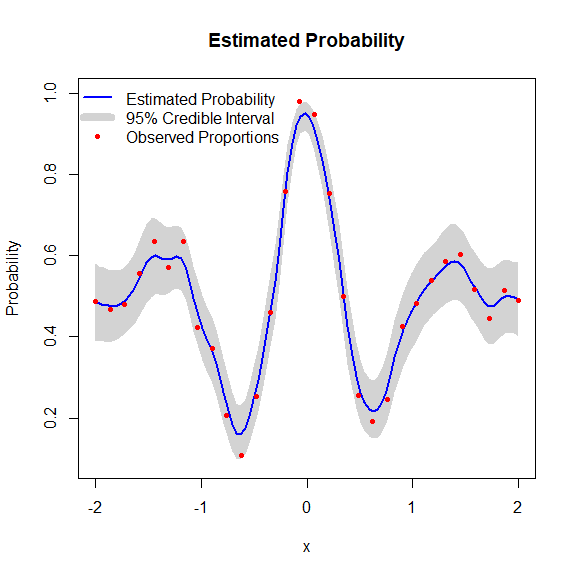

DKP: Multi-class Extension

DKP generalizes BKP to multi-class settings using a Dirichlet-multinomial model.

Example 

# Simulate 3-class data
set.seed(123)
n <- 30
Xbounds <- matrix(c(-2, 2), nrow = 1)
x <- matrix(seq(-2, 2, length.out = n), ncol = 1)
pi1 <- (1 + exp(-x^2) * cos(10 * (1 - exp(-x)) / (1 + exp(-x)))) / 2
pi_true <- cbind(pi1/2, pi1/2, 1 - pi1)

m <- sample(50:100, n, replace = TRUE)
Y <- t(sapply(1:n, function(i) rmultinom(1, size = m[i], prob = pi_true[i, ])))

# Fit DKP model
model_dkp <- fit.DKP(x, Y, Xbounds = Xbounds)

# Predict on new input
Xnew <- matrix(seq(-2, 2, length.out = 10), ncol = 1)
pred_dkp <- predict(model_dkp, Xnew)

# Plot results
plot(model_dkp)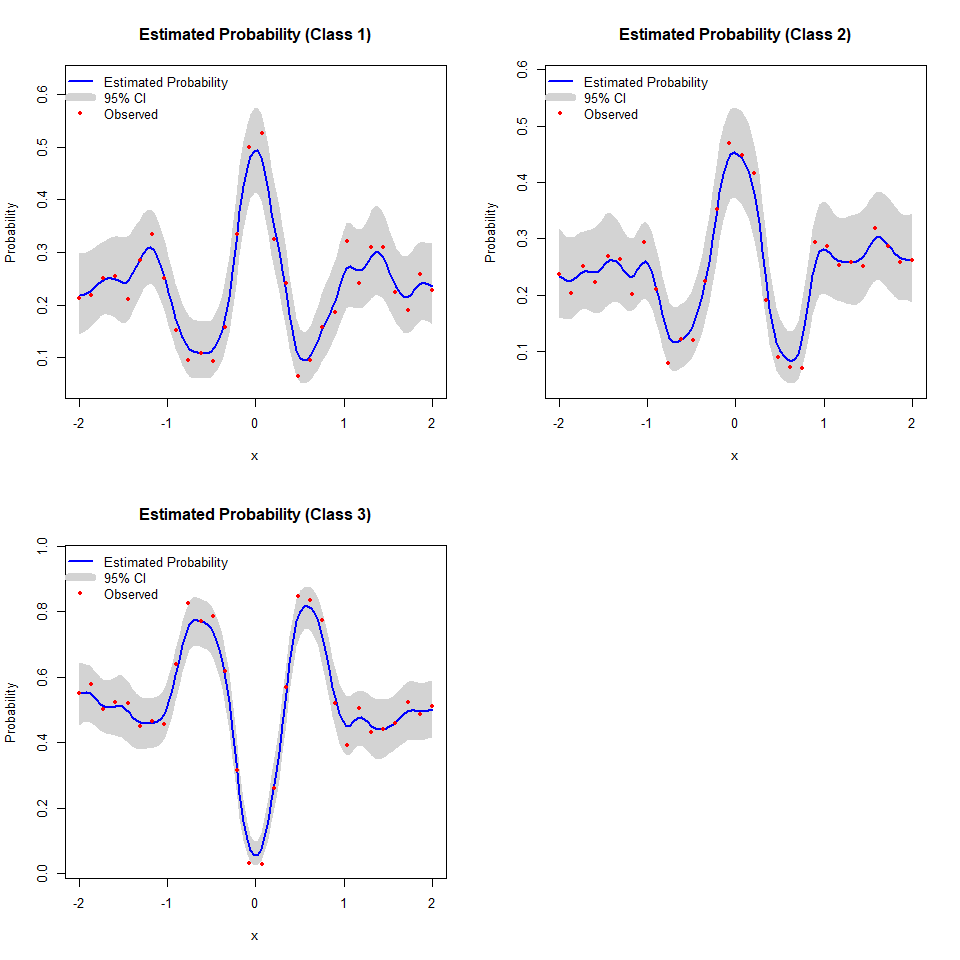

Features

  • ✅ Bayesian modeling for binomial and multinomial count data
  • ✅ Kernel-based local information sharing
  • ✅ Posterior prediction and uncertainty quantification
  • ✅ Class label prediction using threshold or MAP rule
  • ✅ Simulation from posterior (Beta or Dirichlet) distributions

Simulate Posterior Samples

You can simulate posterior samples using:

# BKP posterior draws
simulate(model, Xnew, n_sim = 5)

# DKP posterior draws
simulate(model_dkp, Xnew, n_sim = 5)

Citing

If you use this package in your work, please cite the accompanying methodology papers or package documentation.

Development

The BKP package is under active development. Contributions and suggestions are welcome via GitHub issues or pull requests.